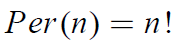Une probabilité P(A) est définie sur un évènement A
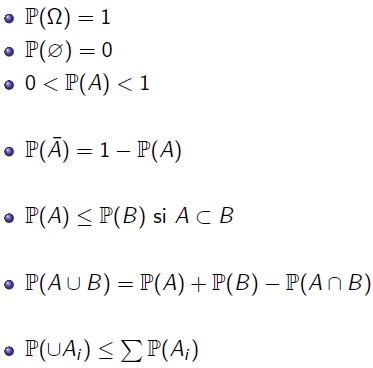
Probabilités conditionnelles
La probabilité conditionnelle d’un évènement A sachant un évènement
B dénote la probabilité de A dans le cas où B est réalisé, notée
P(A|B), et définie par :

On a alors :
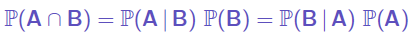
Remarque : P(A et B) est symétrique, P(A|B) ne l’est pas. On vérifie
que P(B) définit bien une probabilité.
Évènements indépendants
A est indépendant de B si P(A|B) = P(A)
c’est-à-dire la connaissance de B ne change pas les “chances” de
réalisation de A
A est indépendant de B => B est indépendant de A
Si A and B sont indépendants, alors :
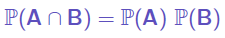
Théorème de Bayes
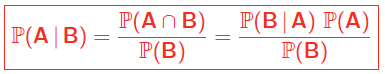
Par la formule des probabilités totales :
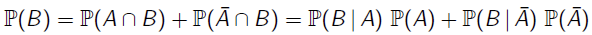
D’où :
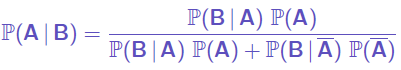
Vous venez de passer un test pour le dépistage du cancer.
Le médecin vous convoque pour vous annoncer le résultat : mauvaise
nouvelle, il est positif. Pas de chance, alors que ce type de cancer ne
touche que 0.1% de la population.
Vous lui demandez si le test est fiable. Sa réponse est sans appel :
« Si vous avez le cancer, le test sera positif dans 90% des cas ; alors que
si vous ne l’avez pas, il sera négatif dans 97% des cas ».
Selon vous, après le résultat d’un tel test,
quelle est la probabilité que vous ayez le cancer ?
A) > 90%
B) = 90%
C) = 9%
D) < 5%
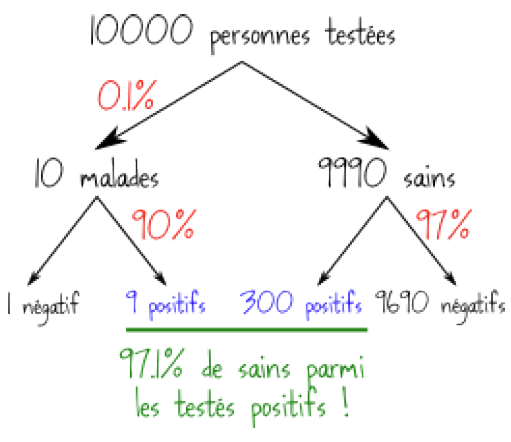
Explications :
Sur les 309 personnes qui sont testées positives, 9 seulement sont réellement malades, et 300 sont saines : ces 300 sont ce qu’on appelle des faux positifs.
Si vous êtes positif, vous n’avez donc que 9/309 = 2.9% de risque d’être réellement malade, et donc 97.1% de chance d’être un faux positif, et donc d’être sain.
Analyse combinatoire
Nous rappelons ici quelques résultats :
• Nombre d’arrangements de p objets pris parmi n avec répétition
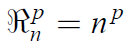
• Nombre d’arrangements de p objets pris parmi n sans répétition
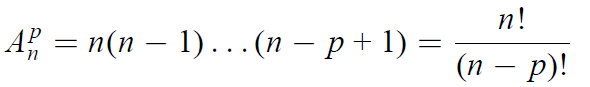
• Nombre de combinaisons de p objets pris parmi n avec répétition
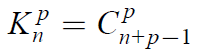
• Nombre de combinaisons de p objets pris parmi n sans répétition
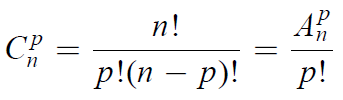
• Nombre de permutations de n objets