Pour évaluer la confiance que l’on peut avoir en une valeur, il est nécessaire de déterminer un intervalle contenant, avec une certaine probabilité fixée au préalable, la vraie valeur du paramètre : c’est l’estimation par intervalle de confiance.
Dans de nombreuses situations, on souhaite connaître la valeur d’une grandeur permettant de caractériser une population statistique pour une variable donnée. Si par exemple la variable étudiée est la taille, on peut chercher à caractériser la population des étudiants de l’Université de Bourgogne par la taille moyenne (“ordre de grandeur” de la taille) et par la variance de cette taille (mesure de la variabilité de la taille). La taille moyenne et la variance de la population sont des paramètres. Ce sont les valeurs qui nous intéressent. Mais la plupart du temps, nous ne les connaissons pas. Nous approchons ces valeurs par la moyenne et la variance de la taille calculées à partir d’un échantillon.
Ces valeurs calculées à partir des données de l’échantillon sont appelées des estimations.
On distingue 2 types d’estimations : les estimations ponctuelles et les estimations par intervalle.
A) Estimation ponctuelle
On prélève un échantillon de n individus, et on mesure le caractère X sur chacun de ces individus. La
moyenne calculée à partir des données d’un échantillon ( Xbar ) est une estimation ponctuelle de la
moyenne de la population (μ).
Un autre échantillon aurait sans doute donné une autre estimation (valeur estimée) pour μ.
La variance calculée à partir des données d’un échantillon (s2X) est une estimation ponctuelle de la
variance de la population (σ2).
Ainsi, 10 échantillons tirés de la même population peuvent fournir 10 estimations ponctuelles (par
exemple de la moyenne de la population), pas nécessairement toutes de mêmes valeurs.
(Cf distribution d’échantillonnage de la moyenne)
Problème : obtention d’une estimation ponctuelle avec n’importe quel échantillon. Quel niveau de
confiance peut-on avoir dans cette valeur?
Une solution : Plutôt qu’une valeur (une estimation ponctuelle) on préfère généralement fournir
une fourchette (un intervalle) calculé à partir de l’échantillon qui va contenir la vraie valeur du
paramètre d’intérêt (la moyenne μ dans la population) avec une confiance (une probabilité) fixée
et contrôlée.
Comparaison de 2 distributions échantillonnage de la moyenne (faible et forte dispersion) : importance de la variabilité dans la population (σ2)et de la taille de l’échantillon (n). (Illustration graphique au tableau)
B) Estimation par intervalle
Une estimation par intervalle est un intervalle défini par 2 bornes dans lequel on a une certaine probabilité de trouver la valeur du paramètre estimé. On parle d’intervalle de confiance.
Nous ne traiterons ici que de l’intervalle de confiance de la moyenne et de l’intervalle de confiance d’une proportion.
B.1) Intervalle de confiance pour une moyenne.
On distingue généralement deux situations : celle où la taille ‘n’ de l’échantillon est relativement faible (n < 30) de celle où on dispose de suffisamment d’observations (n>=30 ) pour pouvoir appliquer des théorèmes « limites » (tel que le théorème de la limite centrale).
Cas de grands échantillons (n>=30)
La distribution d’échantillonnage de la moyenne suit approximativement une distribution normale de moyenne μ et d’écart-type (σ/√n) (Ceci est vrai si n >= 30 individus). On peut donc transformer cette variable X en une variable centrée réduite (qui suit approximativement une distribution normale de moyenne 0 et d’écart-type 1). L’écart-type σ dans la population est souvent inconnu, on le remplace par l’estimateur de l’écart type s.
On arrive ainsi à la formule de l’intervalle de confiance de la moyenne : (illustration graphique au tableau)
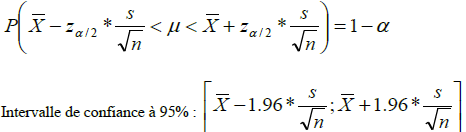
95% = niveau de confiance
Exercice : Quel intervalle si niveau de confiance = 99% ?
Par exemple, imaginons l’intervalle de confiance à 95% de la moyenne suivant : [120 ; 140]. La probabilité que cet intervalle contienne la valeur de μ est de 0,95. Autrement dit, en affirmant que la moyenne de la population est comprise entre 120 et 140, on a 95% de chances d’avoir raison, mais également 5% de chances d’avoir tort. (En fait, une fois les limites de l’intervalle de confiance calculées, soit cet intervalle contient la valeur de μ, soit il ne la contient pas).
La largeur de l’intervalle de confiance est une mesure de la précision de l’estimation. (Plus l’intervalle est étroit, plus l’information que l’on donne est précise.) Affirmer que le poids moyen des cerfs de la forêt de Citeaux est de 200kg avec un intervalle de confiance de [180 ; 220] permet de fournir une information de bien meilleure qualité qu’en disant que ce poids moyen est de 210 kg avec un intervalle de [100 ; 300].
RQ : il existe un compromis entre le niveau de confiance et la précision de l’estimation.
(Si on veut prendre moins de risque, il suffit d’élargir l’intervalle de confiance pour diminuer la probabilité de se tromper).
Cas de petits échantillons (n<30)
Les hypothèses du théorème d’approximation de la distribution de ‘xbar’par une loi normale ne sont plus valides.
Cependant, si on sait que la variable étudiée suit une loi normale , on peut montrer qu’on peut construire quand même un intervalle de confiance en utilisant une loi de probabilités appelée loi de Student . Il s’agit d’une distribution qui est proche de celle de la loi normale centrée réduite. Comme la loi normale centrée réduite, elle est symétrique par rapport à 0. En revanche elle dépend de paramètres (des nombres entiers) qui sont appelés degrés de liberté (ddl).
Pour cela, on remplace le coefficient ‘za/2‘ (le quantil e d’ordre ‘1- a/2’ d’une loi normale centrée réduite) dans l’IC construit pour les grands échantillons par le coefficient ta/2 (le quantile d’ordre 1-a/2 d’une loi de Student à n-1 ddl) pour obtenir au final:
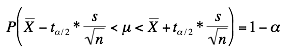
Exemple: Un collectionneur de papillons a prélevé 20 cocons d’une variété de papillons et les a pesés. Il obtient, sur cet échantillon de 20 cocons, un poids moyen de 0.69g et une variance (corrigée) de 0.0109 Pour construire un intervalle de confiance 0.95, il faut chercher dans la table le quantile d’ordre 0.975 d’une loi de Student à 19=20 1 degré de liberté. On trouve =2.093 (à noter que ce coefficient est plus grand que la valeur 1.96 utilisée pour les grands échantillons) et donc l’intervalle de confiance 95%:
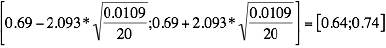
B.1) Intervalle de confiance pour une proportion.
On s’intéresse maintenant à l’estimation par intervalle d’une proportion p dans une population (la proportion de femelles dans une population de souris, la proportion de chênes centenaires qui meurent chaque année dans une région donnée, la proportion de tortues qui atteignent l’âge de 6 mois, …).
On dispose pour cela d’une échantillon de taille n et on note ‘p bar’la proportion calculée dans l’échantillon.
Si on dispose de suffisamment d’observations (n>=30) et que l’ événement étudié est suffisamment observé (np>=5), on peut alors appliquer de nouveau le théorème de la limite centrale et déduire que ‘p bar’ est approximativement distribué comme une loi normale de moyenne p et d’écart type
√p(1-p)/n .
On en déduit l’intervalle, de confiance approximativement égale à ‘1-a’ suivant
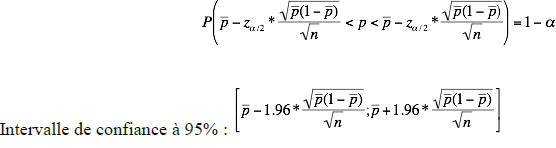
Exemple : Une étude biologique laisse supposer que le pourcentage de sujets de groupe sanguin A dans un population particulière est p=40%. On se propose de s’en assurer en par un sondage sur un échantillon de n= 800 personnes choisies au hasard dans la population étudiée. On observe 360 individus du groupe A.
Construisons un IC de confiance 99% pour p à l’aide de ces mesures. Les conditions sont bien vérifiées sur la taille de l’échantillon et le nombre de cas observé sont bien vérifiées. On a donc l’intervalle (avec za/2=2.576), de confiance 0.99, pour la vraie proportion p dans la population,
[0.405 ;0.495].
Le modèle des biologistes est peut être à remettre en cause, la probabilité que p soit en dehors de l’intervalle [0.405 ;0.495] n’est que de 1%.
Quelques remarques
* On peut dire qu’un intervalle est d’autant plus précis que son amplitude (la longueur de l’intervalle) est petite.
* On peut constater que l’amplitude d’un intervalle de confiance diminue avec la taille d’échantillon :
plus on dispose d’un échantillon (des observations d’une variable effectuées de manière indépendante) de taille importante, plus on dispose d’information sur la distribution (et donc sur sa moyenne) de la variable.
* En revanche, l’amplitude est d’autant plus grande que la confiance qu’on souhaite accorder à l’intervalle est proche de 100%. Sur un même jeu de données, un intervalle de confiance 95% est plus grand qu’un intervalle de confiance 90%, puisqu’on accepte de prendre 5% de risque en plus de ne pas contenir la vraie valeur.
* Enfin, pour la loi normale, on remarque également que l’amplitude est proportionnelle à l’écart type (estimé). L’intervalle de confiance pour la moyenne d’une variable très dispersée (écart type grand) sera plus ample que l’intervalle de confiance d’une variable dont les valeurs sont concentrées autour de la moyenne (écart type faible).
