Généralités sur la statistique

La statistique constitue un pilier fondamental de la méthode scientifique, impliquant la collecte, l’analyse, l’interprétation et la présentation des données. Cette discipline, à la croisée de la science, de la méthode et de la technique, vise à simplifier la complexité des données pour les rendre accessibles à tous. Elle joue un rôle crucial dans la description des phénomènes, la prévision de leurs évolutions futures et la prise de décisions éclairées. Sa polyvalence permet son application dans une multitude de domaines, tels que l’économie, la biologie, la psychologie et les sciences de l’ingénieur, justifiant ainsi son enseignement universel.

La démarche statistique comprend plusieurs étapes clés :

• La collecte des données : cette première étape consiste à rassembler les informations nécessaires à l’étude.
• La présentation des données : il s’agit de structurer les données collectées de manière claire et ordonnée pour faciliter leur analyse.
• L’analyse et la synthèse : cette étape permet de tirer des conclusions significatives sur la population étudiée et de supporter la prise de décision.
• La prévision : lorsque les données présentent une dimension temporelle, l’objectif est de prédire les tendances futures.

La statistique descriptive s’attache à révéler les caractéristiques d’un ensemble d’observations, souvent issues d’expérimentations. L’approche initiale à ces données est exploratoire, visant à établir un premier contact et à comprendre leur structure.

Exemple illustratif : La durée de vie des lampes

Considérons l’étude menée par un fabricant pour déterminer l’impact du type de filament sur la longévité des ampoules. En testant quatre variantes de filaments à travers des échantillons d’ampoules, l’objectif est de comparer les durées de vie obtenues afin de sélectionner le meilleur matériel.

Concepts fondamentaux en statistique

• Population : la notion de population en statistique englobe tout groupe d’unités (ou individus) faisant l’objet de l’étude, désigné par Ω. Historiquement ancrée dans l’étude des populations humaines, cette notion s’étend à tout ensemble d’intérêt pour le chercheur, qu’il s’agisse d’objets, de phénomènes ou de sujets d’étude divers.
• Individu (unité statistique) : chaque élément constitutif de la population est considéré comme une unité statistique, participant à l’ensemble des observations.
• Caractère (variable statistique) : le caractère représente une propriété mesurable ou observable des unités statistiques, susceptible de varier d’un individu à l’autre. Selon sa nature, un caractère peut être qualitatif (par exemple, la nationalité ou la couleur des yeux) ou quantitatif (tel que la taille ou la température).
• Modalités : les modalités désignent les différentes valeurs ou catégories que peut prendre un caractère statistique. Elles reflètent les divers états ou classifications possibles pour chaque caractéristique étudiée. Par exemple, la “situation familiale” peut se décliner en “célibataire”, “marié” ou “divorcé”; de même, le “statut d’un interrupteur” s’exprime par les modalités “0” (éteint) et “1” (allumé).

Types de caractères statistiques

En statistique, les caractères (ou variables) sont classés en deux grandes catégories selon la nature des informations qu’ils représentent : les caractères qualitatifs et les caractères quantitatifs.

Caractères qualitatifs

Les caractères qualitatifs décrivent des attributs ou des qualités qui ne s’accompagnent pas d’une hiérarchie naturelle ou d’un ordre numérique. Ces caractéristiques sont généralement catégorisées et non quantifiables en termes numériques.

Définition : Les caractères qualitatifs sont représentés par des modalités textuelles ou symboliques plutôt que par des nombres.

Exemple : Considérons l’état d’une maison qui peut se décrire par les modalités suivantes :

• Ancienne
• Dégradée
• Nouvelle
• Rénovée

Ces modalités ne suggèrent pas un ordre naturel et ne peuvent être quantifiées directement par des chiffres.

Caractères quantitatifs

À l’opposé, les caractères quantitatifs sont ceux qui peuvent être exprimés et ordonnés en termes numériques. Ils se divisent en deux sous-catégories : discrets et continus.

Définition : Un caractère quantitatif prend des valeurs numériques permettant des opérations mathématiques telles que des comparaisons ou des calculs.

• Discret : Ce type concerne des valeurs distinctes et séparées. Par exemple, le nombre d’enfants dans une famille est un caractère discret car il peut être compté de manière précise.

Exemple :

• Salaire d’employés : 10 000 DA, 20 000 DA, etc. Ces montants précis en font une variable discrète.
• Continu : Les caractères continus concernent des mesures qui peuvent prendre n’importe quelle valeur dans un intervalle donné. Ils reflètent des quantités mesurables et non dénombrables précisément.

Exemple :

• La rigidité des ressorts : entre 10 et 20 N/m. Ce caractère est continu car il peut prendre une infinité de valeurs dans l’intervalle spécifié.

Variable statistique discrète

Une variable discrète se caractérise par un ensemble fini ou dénombrable de valeurs. Chaque observation peut être clairement comptée et distincte des autres.

Formulation : Pour une population Ω, une variable discrète X peut être définie par X : Ω → {x1, x2, …, xn}, où Card(Ω) représente le nombre d’individus dans l’étude.

Exemple concret : Dans une enquête sur le nombre d’enfants par famille dans un village, Ω représente l’ensemble des familles, ω une famille spécifique, et X(ω) le nombre d’enfants dans cette famille.

Analyse des données discrètes

L’analyse de variables discrètes comprend le calcul d’effectifs cumulés, de fréquences cumulées et de fréquences relatives pour résumer et interpréter les données. Ces mesures aident à comprendre la distribution des valeurs au sein de la population étudiée et facilitent la visualisation des tendances et des patterns à travers des représentations graphiques comme les histogrammes ou les diagrammes en bâtons.

La distinction entre caractères qualitatifs et quantitatifs est fondamentale en statistique, car elle détermine les méthodes d’analyse et de représentation des données. La compréhension de ces concepts permet d’approcher les données de manière structurée et de tirer des conclusions significatives à partir d’analyses rigoureuses.

Représentation graphique des séries statistiques et le polygone des fréquences

La représentation graphique joue un rôle crucial dans l’analyse statistique, surtout pour les étudiants débutants. Elle permet de visualiser des données complexes de manière intuitive, facilitant ainsi leur compréhension et leur interprétation. Parmi les diverses méthodes de représentation, nous allons nous concentrer sur deux types principaux : les diagrammes (ou graphiques) et les polygones des fréquences.

Diagrammes et graphiques

Les diagrammes et graphiques offrent une représentation visuelle des données qui aide à en révéler les tendances, les distributions et les comparaisons. Voici quelques-uns des types les plus couramment utilisés :

• Histogrammes : Utilisés pour les données quantitatives continues, ils présentent la distribution des données en regroupant les valeurs en classes ou intervalles. Chaque barre de l’histogramme représente la fréquence (ou l’effectif) des données dans chaque classe.
• Diagrammes en bâtons : Semblables aux histogrammes, mais utilisés pour les données discrètes, ils montrent la fréquence de chaque valeur ou catégorie avec des barres séparées.
• Diagrammes circulaires (ou camemberts) : Pertinents pour représenter des données qualitatives, ils illustrent les proportions de différentes catégories au sein d’un ensemble par des segments d’un cercle.

Polygone des fréquences

Le polygone des fréquences est une autre méthode graphique essentielle en statistique. Il représente la distribution des fréquences d’une série statistique et est particulièrement utile pour comparer les distributions de deux séries ou plus sur le même graphique.

Pour créer un polygone des fréquences, suivez ces étapes :

1. Choisir une échelle appropriée pour les axes : l’axe horizontal (abscisses) représente les classes ou les valeurs de la variable étudiée, tandis que l’axe vertical (ordonnées) indique les fréquences (effectifs ou pourcentages).
2. Marquer les points : Pour chaque classe ou valeur, placez un point au-dessus du milieu de la classe sur l’axe horizontal à une hauteur égale à la fréquence de la classe sur l’axe vertical.
3. Relier les points : Connectez les points consécutifs par des lignes droites. Pour les séries continues, il est d’usage de commencer et de terminer le polygone par des points sur l’axe horizontal à la fréquence zéro, formant ainsi une figure fermée.

Le polygone des fréquences offre une visualisation claire de la forme de la distribution des données, mettant en évidence les modes, les asymétries et d’autres caractéristiques importantes. Il est particulièrement utile pour les étudiants en première année (L1) car il fournit une méthode intuitive pour comparer les distributions et comprendre les concepts statistiques fondamentaux.

En intégrant ces représentations graphiques dans l’analyse de données, les étudiants peuvent non seulement améliorer leur compréhension des séries statistiques, mais aussi développer leur capacité à communiquer efficacement les résultats d’une analyse statistique.

Paramètres de position

Les indicateurs de tendance centrale ou de position les plus fréquemment utilisés sont :

• Le mode est la valeur la plus fréquente dans un jeu de données. Lorsque des données présentent plusieurs modes, on parle de distribution bimodale ou multimodale. Le mode est particulièrement utile pour identifier la catégorie ou valeur dominante dans un ensemble de données qualitatives.
• La médiane correspond à la valeur qui se trouve au milieu d’un jeu de données ordonné. La moitié des observations se situe au-dessous de la médiane et l’autre moitié au-dessus. La médiane est robuste aux valeurs extrêmes, ce qui la rend particulièrement utile pour les distributions asymétriques.
• La moyenne est calculée en additionnant toutes les valeurs d’un jeu de données puis en divisant le total par le nombre d’observations. Elle est sensible aux valeurs extrêmes et est souvent utilisée pour des données quantitatives symétriquement distribuées.

Paramètres de dispersion (variabilité)

Les mesures de dispersion courantes incluent :

• L’étendue mesure la différence entre la plus grande et la plus petite valeur dans un jeu de données, fournissant une estimation simple de la dispersion.
• La variance quantifie la variabilité des données autour de la moyenne. Elle est calculée comme la moyenne des carrés des écarts à la moyenne. Plus la variance est grande, plus les données sont dispersées.
• L’écart type est la racine carrée de la variance et s’exprime dans les mêmes unités que les données. Il offre une mesure de la dispersion des données autour de la moyenne.

Variable statistique continue

Une variable continue peut prendre une infinité de valeurs dans un intervalle donné. Sa représentation graphique la plus courante est l’histogramme des fréquences, où les valeurs sont regroupées en classes et chaque classe est représentée par une barre dont la hauteur est proportionnelle à la fréquence des observations dans cette classe.

Fonction de répartition

La fonction de répartition, notée F(x), décrit la probabilité qu’une variable aléatoire X prenne une valeur inférieure ou égale à x. Elle est cruciale pour comprendre la distribution cumulée des données.

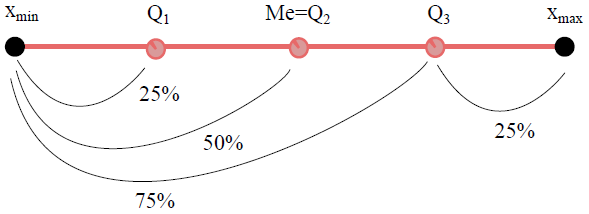
Quartiles

Les quartiles divisent un jeu de données ordonné en quatre parties égales. Le premier quartile (Q1) correspond à la valeur en dessous de laquelle se trouve 25 % des données, le deuxième quartile (Q2) est la médiane, et le troisième quartile (Q3) est la valeur en dessous de laquelle se situe 75 % des données. Les intervalles interquartiles, notamment [Q1, Q3], offrent une vue sur la dispersion centrale des données et aident à identifier les valeurs atypiques.

…..

Paramètres de position

Les indicateurs statistiques de tendance centrale (dits aussi de position) considérés fréquemment sont la moyenne, la médiane et le mode.

Le mode…
La médiane….
La moyenne….

Paramètres de dispersion (variabilité)

Les indicateurs statistiques de dispersion usuels sont l’étendue, la variance et l’écart-type.
…

variable statistique continue

Nous rappelons qu’une variable statistique (V.S) quantitative concerne une grandeur mesurable. Ses valeurs sont des nombres exprimant une quantité et sur lesquelles les opérations arithmétiques (addition, multiplication, etc,…) ont un sens. Nous allons dans ce chapitre se focaliser sur la V.S quantitative continue.

Caractère continu…
Classe de valeurs…
Nombre de classes….
Représentation graphique d’un caractère continu
Histogramme des fréquences…

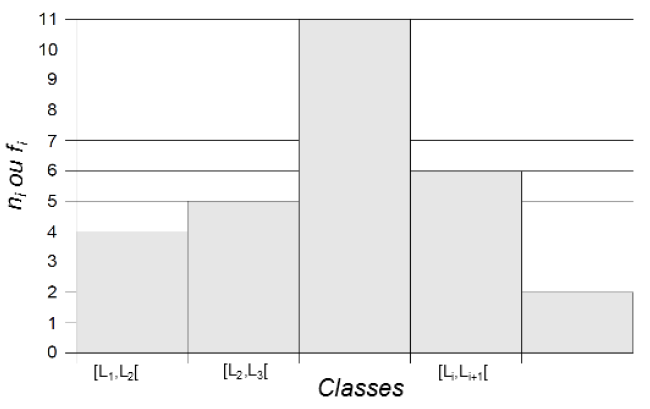
Nous pouvons représenter le tableau statistique par un histogramme. Nous reportons les classes sur l’axe des abscisses et, au-dessus de chacune d’elles, nous traçons un rectangle dont l’aire est proportionnelle à la fréquence f_i (ou l’effectif n_i) associée. Ce graphique est appelé l’histogramme des fréquences.

Fonction de répartition
La moyenne

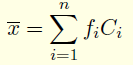
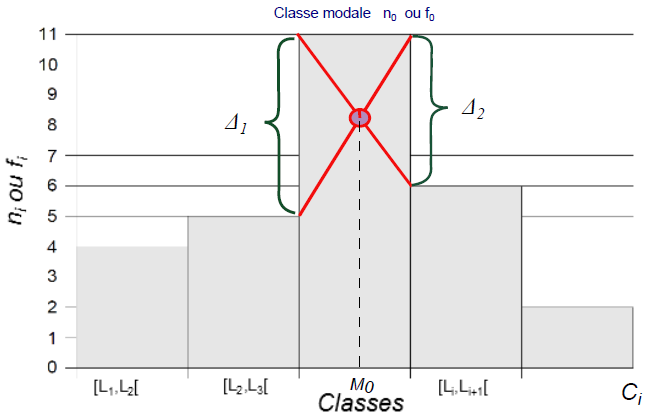
Le mode
La définition suivante permet de comprendre la démarche à suivre pour calculer le mode d’une manière exacte et qui se trouve dans une des classes appelée “classe modale”.

La médiane

F(x) = (f_i+1 / h) (x-L_i) + F_i

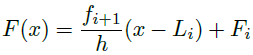
Paramètres de dispersion

La variance

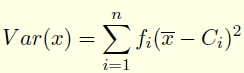
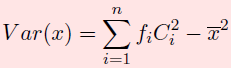
l’écart type: σ _X = √ Var (x)

Pour i ϵ {1, 2, 3}, la quantité Q_i tel que F(Q_i) = 1/4 s’appelle le i^em quartile.

Exemple :
Pour i = 2, Q₂ tel que F(Q₂) = 2/4 = 0.5 , donc, Q₂ = Me.

La détermination ou le calcul de Q_i se fait exactement comme le calcul de la médiane (graphiquement ou analytiquement).

Interprétation : Il y a 25 % d’individus dont la valeur du caractère est dans l’intervalle [a₀,Q₁]. De même pour les autres quartiles.
Ces intervalles s’appellent “intervalles interquartiles”.
Q1 -> 25%
Q2 -> 50%
Q3 -> 75%

-> Retour à la page d’accueil <-