A) Notion de variable aléatoire
On considère ici comme acquises les bases des calculs de probabilité. Nous allons voir maintenant comment ces probabilités peuvent nous permettre de prédire les valeurs attendues pour des variables aléatoires dans le domaine de la biologie.
Une variable aléatoire (notation X) est une donnée dont on ne peut prédire la valeur exacte pour un individu avant d’avoir réalisé la mesure, l’observation, l’expérience sur cet individu. Ceci n’implique pas nécessairement qu’on ait aucune idée de la valeur (ou de la gamme de valeur) à laquelle on peut s’attendre.
Ex : Jet d’un dé et X = nb affiché par le dé
Jet d’une pièce de monnaie et X = Pile ou Face
Jet de 2 dés et X = somme des nb affichés par les 2 dés
Mais aussi : X = Sexe d’un singe à la naissance
X = Taille d’un chêne à l’âge de 20 ans
X = Couleur des cheveux d’un étudiant
X = Statut sanitaire d’un oiseau dans une forêt (parasité ou non, malade ou non)
On considère en général 2 classes de variables aléatoires : discrètes et continues.
Variable aléatoire discrète :
ne peut prendre que certaines valeurs dans un intervalle donné
Ex : nb de fois “pile” sur 10 lancers d’une pièce de monnaie, nb de poussins dans une nichée, proportion de femelles dans une nichée de 12 poussins
Variable aléatoire continue :
peut prendre toutes les valeurs possibles dans un intervalle donné. De plus la probabilité d’observer une valeur exacte est de 0 (un étudiant peut mesurer entre 1.60m et 1.90m, mais la probabilité qu’il mesure exactement 1.752132652414 est de 0).
B) Variable aléatoire discrète
1.Fonction de densité
Le “comportement” d’une variable aléatoire discrète est décrit par une fonction mathématique appelée distribution de probabilité ou fonction de densité ou loi de probabilité. Cette fonction précise quelles valeurs peut prendre la variable étudiée, et avec quelles fréquences. Elle associe en fait une probabilité à chaque valeur de la variable aléatoire.
Définition
Soit X la variable aléatoire discrète. La distribution de probabilité ou fonction de densité de probabilité f pour X est :
f(x) = P(X = x)
avec x : un nombre réel
f est définie pour tous les réels
f(x) >=0 car c’est une probabilité
f(x) = 0 pour la plupart des réels car X est une variable discrète
la somme des f(x) pour toutes les valeurs de X est égale à 1 :
∑ f(x)=1
Espérance mathématique
Supposons qu’on effectue 1000 lancers de 1 dé. Quelle serait le nb moyen obtenu sur ces 1000 lancers?
Supposons qu’on effectue 50000 lancers de 2 dés. Même question?
Déterminer ces valeurs de manière empirique serait extrêmement fastidieux. La fonction de densité peut être utilisée pour déterminer a priori ces valeurs, que l’on appelle alors une espérance
mathématique et que l’on note E(X).
Définition
µ = E(x)=∑xi.f(xi)
En d’autres termes, chaque valeur de X est pondérée par sa densité (probabilité) (Cf parallèle avec
calcul de la moyenne pour des données groupées en classes).
On parle de moyenne ou d’espérance mathématique. Il s’agit en effet de la valeur moyenne observée si on répétait l’expérience un grand nombre de fois.
Exemple : X = nb affiché par 1 dé à 6 faces (dé équilibré)
µ = ∑x.f(x)=1*1/6+2*1/6+….+6*1/6=21/6=3.5
Exercice: Quelle est la valeur moyenne attendue pour la variable aléatoire X définie comme la
somme des nb affichés par 2 dés équilibrés si on effectue 1000 lancers.
Réponse : μ = 7
Ce résultat est assez intuitif. On lance 2 dés, on attend donc le double de la moyenne attendue avec 1
seul dé.
E(X+Y) = E(X) + E(Y) = 3.5 + 3.5 = 7
Définition
On peut généraliser l’espérance mathématique. Soit H(X) une fonction de la variable aléatoire discrète
X.
E [H(X)] =∑H(x).f(x)
Variance
En plus de déterminer a priori la moyenne attendue d’une variable aléatoire discrète, on peut déterminer la variabilité autour de cette moyenne, c’est-à-dire la variance.
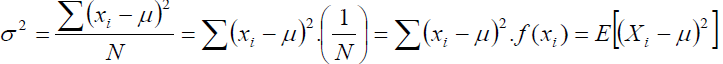
f(xi)=1/N car il y a N valeurs dans la population
En développant :
E[(X-μ)2] = E(X2) – E(2Xμ) + E(μ2)
= E(X2) -2μE(X) + E(μ2)
= E(X2) -2μ.μ + E(μ2)
= E(X2) -2μ.μ + μ2
= E(X2) -μ2
= E(X2) – [E(X)]2
=> σ2 = E(X2) – [E(X)]2
Exemple : 1 dé
σ2 = E(X2) – μ2 = 15.167 – (3.5)2 = 2.917
Si X = 2 dés
σ2 = E(X2) – μ2 = 54.833 – (7)2 = 5.833
La variance possède aussi quelques propriétés qu’il faut connaître.
V(λX) = λ2V(X)
Si deux variables aléatoires X et Y sont indépendantes : V(X+Y) = V(X) + V(Y)
Mais attention, cette égalité n’implique pas nécessairement que X et Y sont indépendantes.
Exercice: Les couples de merle d’Amérique Turdus migratorius produisent en général des nichées de 3 à 6 oeufs. Supposons que la fonction de densité estimée pour la variable aléatoire X (= nombre d’oeufs par nichée) est donnée dans le tableau suivant.
| Nb d’oeufs : x | 3 | 4 | 5 | 6 |
| Densité : f(x) | 0.35 | 0.45 | 0.16 | 0.04 |
Quelle taille de ponte de moyenne attendez-vous pour une population de merle d’Amérique? Quelle variabilité de la taille de ponte attendez-vous autour de cette valeur moyenne?
Interprétation de la fonction de densité : probabilité pour un couple tiré au hasard, et % dans la population
μ=E(X)= ∑x.f(x)= 3(0.35)+4(0.45)+5(0.16)+6(0.04) = 3.89
σ2 = E(X2) – μ2 = [32 (0.35)+42 (0.45)+52 (0.16)+ 62 (0.04)]–(3.89)2 = 15.79 – 15.13 = 0.66
La taille de ponte moyenne est donc de 3.89 oeufs et son écart-type dans la population est de 0.81 oeufs.
4.Fonction de répartition
Nous venons de voir comment la distribution de probabilité d’une variable aléatoire pouvait nous renseigner sur la probabilité d’observer une valeur précise ou un ensemble de valeurs précises.
Cependant, de nombreux problèmes statistiques nécessitent de connaître, non pas la probabilité d’observer une certaine valeur, mais d’observer une valeur au moins aussi grande (ou aussi petite)
qu’une valeur donnée de X. Au lieu de chercher P(X=x), on chercher P(X≤x).
Exemple : en jetant 2 dés, quel est la probabilité d’observer un total de 5 maximum?
P(X≤5) = [P(X=2) + P(X=3) + P(X=4) + P(X=5)] = 1/36 + 2/36 + 3/36 + 4/36 = 10/36 = 0.28
Le calcul se fait en additionnant les probabilités de tous les évènements individuels qui satisfont à l’évènement d’intérêt. Lorsqu’on a un grand nombre d’évènements individuels, cela peut devenir laborieux.
Dans ces situations, on utilise ce qu’on appelle la fonction de densité cumulée F(x) (CDF), qu’on appelle aussi fonction de répartition:
F(x) = P(X ≤ x)
Exercice: En reprenant l’exemple d’un jet de 2 dés équilibrés, déterminez la fonction de distribution cumulée de la variable aléatoire X (X = somme des nombres affichés par les 2 dés). Déterminez ensuite la probabilité d’obtenir 1) un maximum de 8, 2) une valeur comprise entre 4 et 10?

P(X≤8) = F(8) = 26/36
P(4 < X < 10) = F(9) – F(4) = 30/36 – 6/36 = 2/3
C) Variable aléatoire continue
Définition: La fonction de densité de probabilité pour une variable aléatoire continue X est une fonction f définie pour tous les réels x telle que :
– f(x) ≥ 0
– la région comprise entre le graphe de f et l’axe des abscisses x a une aire de 1
– pour tous réels a et b, P(a ≤ X ≤ b) est donnée par l’aire limitée par le graphe de f, l’axe des abscisses, et les lignes x=a et x=b
Dans un premier temps, nous allons voir que les probabilités peuvent être déterminées de manière géométrique, pour des fonctions simples (cas A, B, C). Pour des fonctions plus complexes (courbes, cas D), on utilisera les calculs d’intégrales.
En voici 3 exemples :
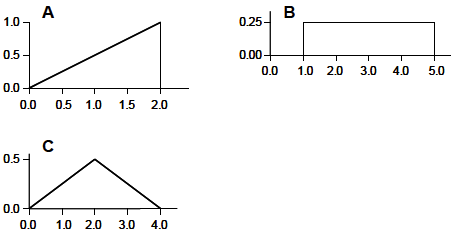
Ces 3 exemples correspondent bien à la définition ci-dessus car :
En A, l’aire du triangle est ½*bh = 1/2*1.0*2.0 = 1.0
En B, l’aire du rectangle est bh = 0.25*4 = 1.0
En C, l’aire du triangle est ½*bh =1/2*4.0*0.5 = 1.0
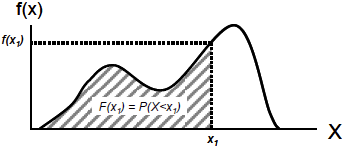
Dans tous les cas; la fonction de densité, notée f(x) correspond à la courbe (ou à la ligne brisée dans les cas simples, mais rarement rencontrés). La fonction de répartition, notée F(x) correspond à une aire située entre cette courbe et l’axe des abscisses.
Exercice: D’après le cas A, trouvez P(X < 1.0) et P(X ≤ 1).
P(X < 1.0) = aire du triangle avec x=1.
P(X < 1.0) = 1/2*0.5*1.0 = 0.25
P(X ≤ 1) = même chose, car pour des variables continues, la probabilité que X prenne une valeur
exacte est égale à 0. (géométriquement, cette probabilité est une ligne et non une aire)
Exercice: Le cas B représente la fonction de densité du poids (en livres) du crapaud buffle Bufo
marinus.
Trouvez:
a) P(X < -1),
b) P(X=2),
c) P(X>2),
d) P(2≤X≤4).
Que signifient ces probabilités?
P(X < -1) = 0 car F (-1) = 0
Il est impossible d’observer un crapaud dont le poids serait inférieur à une valeur négative.
P(X=2) = 0 car cette probabilité correspond à une ligne et non à une aire
La probabilité de capturer dans cette population un crapaud dont le poids exact serait de 2.00000000 livres est nulle.
P(X>2) = aire du rectangle de x=2 à x=5.
P(X>2) = bh = 0.25*3 = 0.75
OU
P(X>2) = 1 – F(2) = 1 – 0.25*1 = 1 – 0.25 = 0.75
75% des crapauds ont un poids supérieur à 2 livres.
P(2≤X≤4) = aire du rectangle de x=2 à x=4
P(2≤X≤4) = bh = 2*0.25 = 0.5
La moitié des individus ont u poids compris entre 2 et 4 livres (limites comprises).
OU
P(2≤X≤4) = F(4) – F(2) = 0.25*3 – 0.25*1 = 0.75 – 0.25 = 0.5
Exercice: Le cas C représente le temps en minutes avant le début d’un choc anaphylactique suivant une piqûre d’abeille chez des enfants allergiques aux piqûres d’abeilles.
Quelle est la probabilité que le choc se manifeste
a) en moins de 2 minutes,
b) en moins de ou au bout d’1 minute,
c) après plus d’1 minute mais en moins de 3 minutes?
Que signifient ces probabilités?
P(X<2) = ½*bh = ½*2*0.5 = 0.5
Dans la moitié des cas, le choc débute dans les 2 premières minutes qui suivent la piqûre.
P(X≤1) = ½*bh = ½*1*0.25 = 0.125
Dans 1 cas sur 8, le choc débute dans la première minute après la piqûre.
P(1<X<3)] = aire zone totale – (triangle de x=0 à x=1 et triangle x=3 à x=4)
P(1<X<3)] = 1 – [P(X<1) + (P(X>3)] = 1 – [(1/2*1*0.25) + (1/2*1*0.25)] = 0.75
75% des enfants subissent un choc entre 1 et 3 minutes après avoir été piqués.
Les mêmes résultats peuvent obtenus si on utilise la fonction de densités cumulées F.
P(1<X<3) = F(3) – F(1)
Lorsque l’on a une fonction de densité complexe (courbe), ce qui représente la plupart des cas
rencontrés en biologie/géologie, on a recours aux calculs d’intégrales. On a en effet :
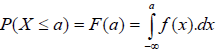
RQ : il s’en suit que P(X=a) = F(a)-F(a) = 0.
(La probabilité qu’un arbre tiré au hasard dans une forêt ait une hauteur de exactement
13.50000000000000000 mètres est nulle)
Les calculs de l’espérance et de la variance font aussi appel aux calculs d’intégrales. MAIS dans
la pratique, on ne fera (heureusement…) jamais ces calculs nous-mêmes!!! Nous verrons par la
suite que nous essaierons de rapprocher les fonctions étudiées de quelques fonctions bien connues
(qu’on appelle parfois les grandes lois), pour lesquels ces calculs ont déjà été faits et dont les résultats
sont fournis dans des tableaux prêt à l’emploi.
