A) Loi Binomiale
En théorie des probabilités et en statistique, la loi binomiale modélise la fréquence du nombre de succès obtenus lors de la répétition de plusieurs expériences aléatoires identiques et indépendantes.
Il s’agit probablement de la loi discrète la plus utilisée en biologie. Elle s’applique des phénomènes qui
répondent aux critères suivants:
1.Une expérience (au sens statistique) est répétée un certain nombre de fois (ce nombre est noté n). 2.Chaque expérience ne peut avoir que 2 issues possibles, mutuellement exclusives (“binomiale” = “2
noms”) : par exemple, “succès” & “échec”
3.La probabilité de “succès” est notée p et reste constante d’une expérience à l’autre. La probabilité
d'”échec” est notée q et est égale à 1-p.
4.Les répétitions de l’expérience sont indépendantes les unes des autres. L’issue d’une expérience n’est aucunement influencée par l’issue de n’importe quelle autre expérience.
La variable aléatoire X à laquelle on s’intéresse est en général le nombre de “succès” obtenus parmi les
n répétitions de l’expérience.
X peut donc prendre les valeurs suivantes : {0, 1, 2, …, n}.
Exemples de phénomènes biologiques obéissant à une loi binomiale :
-nombre de mâles dans les nichées de 10 poussins de mésange bleue
-nombre de droitiers dans une classe de 20 étudiants…
Problème : calculer P(X = x) pour chaque valeur x afin de déterminer la fonction de densité (ou loi de
probabilité de X).
Plusieurs séquences de “succès” et “échec” possibles, avec des nombres différents de “succès”
(différentes valeurs de X)
Il y a Cnx séquences ayant x succès et n-x échecs (nombre de combinaisons de x places (pour
les succès) parmi les n places dans la séquence)
Chacune de ces séquences a une probabilité d’apparaître de px(1-p)n-x (les probabilités de succès
et d’échec sont multipliées car les répétitions sont indépendantes)
Définition: La fonction de densité d’une variable aléatoire binomiale avec n répétitions et une probabilité de succès p est donc :
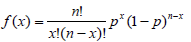
La fonction de densité d’une variable aléatoire binomiale est donc caractérisée par 2 paramètres : n, le
nombre de répétitions, et p, la probabilité de “succès” à chaque répétition de l’expérience.
Espérance mathématique & variance
On peut déterminer la moyenne et la variance d’une distribution binomiale en utilisant les règles de
calculs vues lors des 2 dernières séances.
Si X et Y sont 2 variables aléatoires : E(X+Y) = E(X) + E(Y)
Si X et Y sont 2 variables aléatoires indépendantes : V(X+Y) = V(X) + V(Y)
Chaque répétition de l’expérience étant indépendantes des autres, X peut être considérée comme la
somme de n variables aléatoires pouvant prendre les valeurs 0 ou 1.
X = X1 + X2 + … + Xn =∑ Xi
Chaque Xi a pour espérance : E(Xi)= ∑ xf(x)=1*p+0*(1-p)=p
et pour variance :
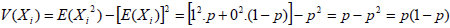
D’où
Espérance mathématique :
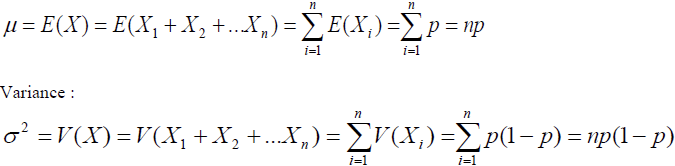
Exercice: En reprenant l’exemple précédent, calculez la moyenne et la variance du nombre de filles
dans une famille de 5 enfants.
Au lieu de calculer la moyenne et la variance à partir de la fonction de densité comme nous l’avons vu
lors des séances précédentes, on peut utiliser les formules propres à la loi binomiale puisque la variable
aléatoire qui nous intéresse suit une telle distribution.
μ = np = 5*0.5 = 2.5
σ2 = np(1-p) = 5*0.5*0.5 = 1.25
Les familles de 5 enfants ont en moyenne 2.5 filles.
RQ : calculs très faciles sans avoir f(x)
La loi binomiale n’est pas toujours symétrique autour de la moyenne (comme dans l’exemple
précédent). Elle n’est symétrique que si p=0.5. Mais plus n augmente, plus la distribution tend à être
symétrique autour de sa moyenne.
B) Loi Normale
Les lois normales sont parmi les lois de probabilité les plus utilisées pour modéliser des phénomènes naturels issus de plusieurs événements aléatoires.
La plupart des variables aléatoires continues rencontrées dans le domaine des sciences de la vie n’ont pas une forme aussi simple que celles vues lors des premières séances (triangle, rectangle…). Elles sont donc un peu plus difficiles à manipuler. Les principes vus précédemment restent néanmoins les mêmes.
La distribution continue la plus rencontrée et donc la plus importante est sans aucun doute la distribution normale.
Cette distribution a la forme d’une courbe en cloche. On parle aussi de courbe de Gauss (et de distribution gaussienne). Il s’agit d’une distribution symétrique.
Cette courbe représente la fonction de densité f(x). La fonction de densité cumulée ou fonction de répartition F(x) correspondante est telle que F(a) = P(X≤a). Il s’agit géométriquement de l’aire située sous la courbe à gauche de la valeur x=a. (Cf graphique au tableau)
L’aire située sous la courbe entre -∞ et +∞ est égale à 1.
L’aire située sous la courbe en cloche comprise entre a et b correspond à la probabilité P(a≤X≤b).
Le calcul de cette probabilité nécessite de calculer :
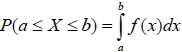
Cette probabilité peut aussi être calculée de la manière suivante :
P(a≤X≤b) = F(b) –F(a)
Mais on a
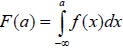
Les calculs nécessitent donc d’utiliser des intégrales sur des intervalles du type]-∞;a]. Heureusement,
nous verrons que ces calculs ont été faits est reportés dans des tables statistiques.
Il ne sera donc pas nécessaire de les faire manuellement.
Petit rappel : P(X=a) = 0, car :
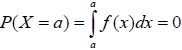
L’équation de la fonction de densité f(x) est la suivante :
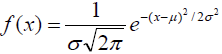
avec σ = écart-type de la distribution et μ = moyenne de la distribution.
Comme la loi binomiale, la loi normale est donc définie par 2 paramètres (σ et μ).
-La courbe en cloche est centrée sur μ. Pour une même valeur de σ, des distributions ayant des valeurs de μ différentes correspondent à des courbes ayant exactement la même forme, mais étant décalées sur l’axe des abscisses.
-La forme de la courbe en cloche dépend de σ. Pour une même valeur de μ, des distributions ayant des valeurs de σ différentes correspondent à des courbes centrées sur le même point, mais étant plus ou moins “aplaties et larges” (μ +/- σ = point d’inflexion).
La distribution normale correspond donc à une famille de distributions, de taille infinie (autant de distributions que de combinaisons de valeurs de μ et σ).
Propriété intéressante :
68% des valeurs comprises entre μ-σ et μ+σ.
environ 95% entre μ-2σ et μ+2σ
environ 95% entre μ-3σ et μ+3σ
Heureusement, on peur ramener toutes ces distributions normales à une distribution normale particulière et unique: la distribution normale centrée réduite.
C) Loi Normale centrée réduite
Si X est une variable aléatoire suivant une distribution normale de moyenne μ et d’écart-type σ, alors la
variable Z = X-μ / σ suit une distribution normale de moyenne 0 et d’écart-type 1.
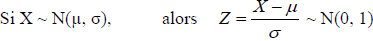
On parle de centrage et de réduction. Z est une variable centrée réduite. (voir graphiquement l’effet de chaque étape)
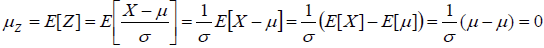
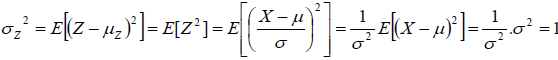
La fonction de densité et la fonction de répartition de la loi normale centrée réduite est parfaitement connue et les valeurs correspondant à ces 2 fonctions ont été compilées dans 2 tables statistiques (que l’on trouve dans tous les livres de statistiques ou sur internet).
Dès qu’on aura à utiliser la fonction de répartition d’une distribution normale, on transformera d’abord cette variable en une variable centrée réduite et on utilisera la fonction de répartition de la loi normale centrée réduite.
Relation entre loi binomiale et loi normale
Si X est une variable aléatoire binomiale B(n,p), alors si n est suffisamment grand, X a approximativement une distribution normale de moyenne np et de variance npq.
Bonne approximation quand np(1-p) > 3
P(X<15) = FB(14) = FN(14.5)
On a ajouté 0.5 à la valeur souhaitée parce qu’on estime une distribution discrète à partir d’une distribution continue. Il s’agit d’une correction de continuité.
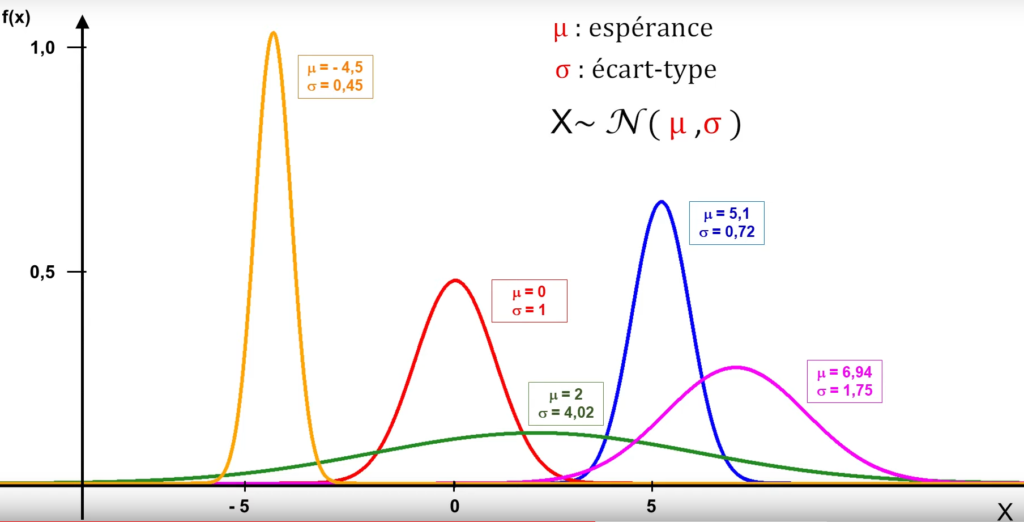
Toute loi normale est entièrement caractérisée par ses deux paramètre exact: la moyenne et l’écart type.
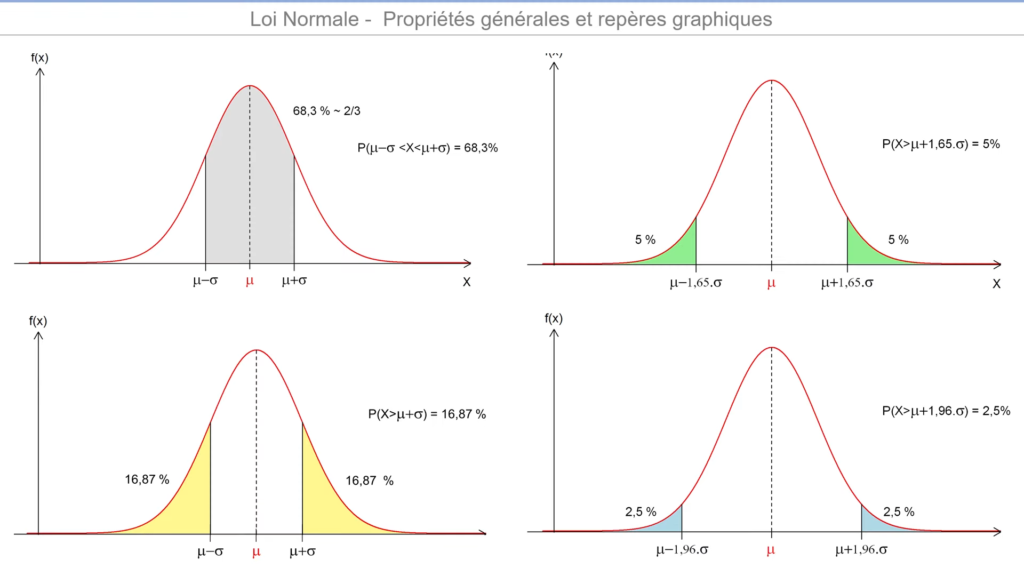
Quelques propriétés caractérisant toutes les lois normales!
– la probabilité que X se trouve à un écart type de la moyenne est d’environ 68%,
– la probabilité que X soit supérieur à μ + 1.65 σ est égale à la probabilité que X soit inférieur à μ -1.65 σ est égale à 5%,
– la probabilité que X soit supérieur à μ + 1.96 σ est égale à la probabilité que X soit inférieur à μ – 1.96 σ est égale à 2.5%.
Tableau Z

